Правильная пирамида развертка.

Правильная пирамида. имеющая в основании правильный n — угольник (в данном случае шестиугольник), показана на рис. 1. Для удобства построения одно из ребер, например O’V’ расположено в плоскости, параллельной фронтальной проекции.

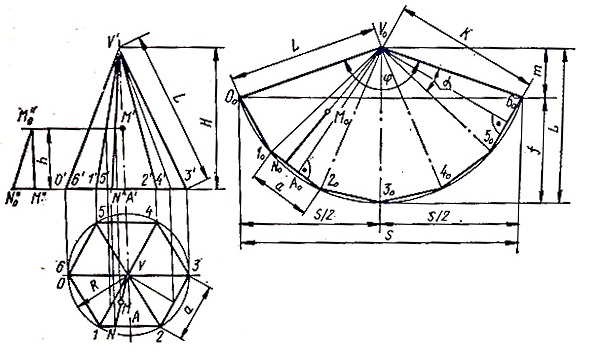
Рис. 1. Правильная пирамида развертка.

Поэтому на рисунке показана его натуральная величина. Построение развертки боковой поверхности следует начинать с произвольной точки V₀, из нее как из центра радиусом, равным длине бокового ребра пирамиды R = L, описывается дуга. От произвольной точки O₀ на дуге n раз последовательно откладывается сторона многоугольника. Полученные точки 0₀, 1₀, …, 6₀ последовательно соединяются между собой и с высотой V₀.

Если дана точка М, принадлежащая одной из плоскостей пирамиды, то ее можно перенести на развертку следующим образом. Проводится прямая MV до пересечения со стороной основания в точке N и соответственно М’V’ до пересечения в точке N’. Расстояние 1N откладывается от точки 1₀ на стороне 1₀2₀ развертки до точки N₀. Проводится прямая N₀V₀. Для определения действительной длины отрезка NM нужно построить вспомогательный прямоугольный треугольник со сторонами N”₀M” = NM и М”М”₀ = h. От точки N₀ откладывается расстояние N”₀M”₀. Получаем точку М₀.

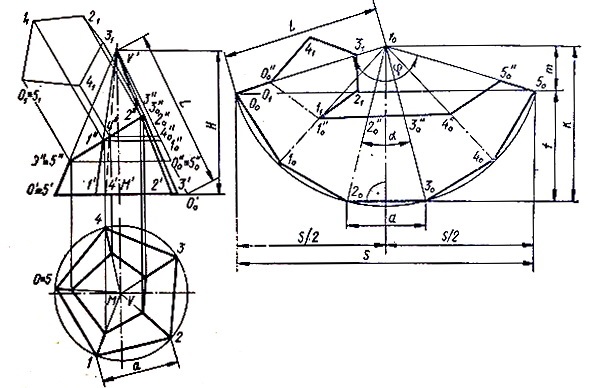
Рис. 2. Правильный пятиугольник усеченный плоскостью.

Для аналитического определения элементов разверток пирамиды используют ряд зависимостей; боковое ребро ,

высота треугольников, составляющих развертку боковой поверхности ; тангенс половины плоского угла при вершине пирамиды:

полный угол развертки ᵠ = nα.

Величины s, m и f можно определить, воспользовавшись зависимостями:

;

.

Для четного количества плоскостей пирамиды (рис. 1):

.

Для нечетного количества плоскостей пирамиды (рис. 2):

.