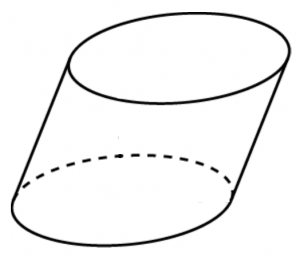
Построение развертки наклонного эллиптического цилиндра с круговыми основаниями.

В статье приведено детальное описание построения развертки наклонного эллиптического цилиндра с круговыми основаниями. Построение по точкам наклонного эллиптического цилиндра.

Цилиндр показан на рис 1. Из центра – произвольной точки S₁ – описывается полуокружность радиусом А, которая делится на равное число частей (в данном случае шесть). Через точки деления 0ꞋꞋ, 1ꞋꞋ,…, 6ꞋꞋ проводятся горизонтальные прямые. Половина круга основания цилиндра также делится на принятое число равных частей. Радиусом равным длине дуги, соответствующей одному делению основания, последовательно делаются засечки, начиная от точки 0⁰₁ на горизонтальных прямых. Получаем точки 1⁰₁,…, 6⁰₁. Их соединяют плавной кривой. Для получения всей развертки строится симметричная ветвь полученной кривой и на расстоянии Н – 2А строится кривая, эквидистантная первой. Ширина развертки L должна быть равна длине эллипса.

Рисунок 1. Развертка наклонного эллиптического цилиндра с круговыми основаниями.

На рисунке также показан способ построения развертки эллиптического цилиндра, усеченного двумя параллельными плоскостями (он аналогичен методу, который показан на рис. 3. в статье развертка цилиндра эллиптического, усеченного наклонной плоскостью). В данном случае может быть применен и аналитический метод.