
Развертка цилиндра эллиптического, усеченного наклонной плоскостью.
Развертка цилиндра эллиптического.
Содержание
Развертка представляет собой прямоугольник длиной L, равной длине эллипса, и высотой H (рис. 1). Длину эллипса можно определить графически способом, показанным на рис. 2. Аналитически полная длина эллипса может быть определена по формуле:
L = аl1,
где
а — большая полуось;
l1 — длина эллипса при a = 1.
Значения l1 даны в табл. 1.
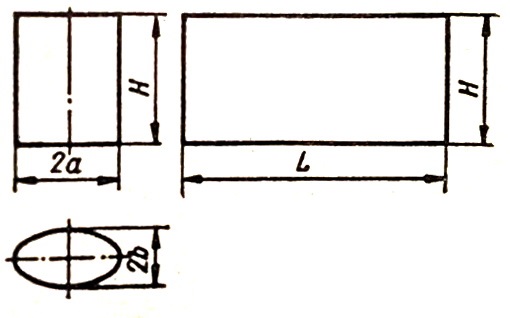
Рис. 1.
.
Таблица 1. Длина эллипса l1 при a=1 в зависимости от b/a.
| b/a | l1 | b/a | l1 | b/a | l1 | b/a | l1 | b/a | l1 |
| 0,00 | 4,0000 | 0,20 | 4,2020 | 0,40 | 4,6026 | 0,60 | 5,1054 | 0,80 | 5,6723 |
| 0,01 | 4,0011 | 0,21 | 4,2186 | 0,41 | 4,6258 | 0,61 | 5,1324 | 0,81 | 5,7020 |
| 0,02 | 4,0038 | 0,22 | 4,2356 | 0,42 | 4,6492 | 0,62 | 5,1596 | 0,82 | 5,7317 |
| 0,03 | 4,0078 | 0,23 | 4,2531 | 0,43 | 4,6728 | 0,63 | 5,1870 | 0,83 | 5,7615 |
| 0,04 | 4,0131 | 0,24 | 4,2710 | 0,44 | 4,6966 | 0,64 | 5,2145 | 0,84 | 5,7915 |
| 0,05 | 4,0194 | 0,25 | 4,2892 | 0,45 | 4,7207 | 0,65 | 5,2421 | 0,85 | 5,8215 |
| 0,06 | 4,0267 | 0,26 | 4,3078 | 0,46 | 4,7450 | 0,66 | 5,2699 | 0,86 | 5,8516 |
| 0,07 | 4,0348 | 0,27 | 4,3268 | 0,47 | 4,7695 | 0,67 | 5,2978 | 0,87 | 5,8819 |
| 0,08 | 4,0438 | 0,28 | 4,3462 | 0,48 | 4,7942 | 0,68 | 5,3259 | 0,88 | 5,9122 |
| 0,09 | 4,0535 | 0,29 | 4,3659 | 0,49 | 4,8191 | 0,69 | 5,3541 | 0,89 | 5,9426 |
| 0,10 | 4,0640 | 0,30 | 4,3859 | 0,50 | 4,8442 | 0,70 | 5,3824 | 0,90 | 5,9732 |
| 0,11 | 4,0752 | 0,31 | 4,4062 | 0,51 | 4,8695 | 0,71 | 5,4108 | 0,91 | 6,0038 |
| 0,12 | 4,0870 | 0,32 | 4,4269 | 0,52 | 4,8950 | 0,72 | 5,4394 | 0,92 | 6,0345 |
| 0,13 | 4,0994 | 0,33 | 4,4478 | 0,53 | 4,9207 | 0,73 | 5,4681 | 0,93 | 6,0653 |
| 0,14 | 4,1125 | 0,34 | 4,4692 | 0,54 | 4,9466 | 0,74 | 5,4969 | 0,94 | 6,0962 |
| 0,15 | 4,1261 | 0,35 | 4,4908 | 0,55 | 4,9726 | 0,75 | 5,5258 | 0,95 | 6,1271 |
| 0,16 | 4,1403 | 0,36 | 4,5126 | 0,56 | 4,9988 | 0,76 | 5,5549 | 0,96 | 6,1582 |
| 0,17 | 4,1550 | 0,37 | 4,5347 | 0,57 | 5,0252 | 0,77 | 5,5841 | 0,97 | 6,1893 |
| 0,18 | 4,1702 | 0,38 | 4,5571 | 0,58 | 5,0518 | 0,78 | 5,6134 | 0,98 | 6,2205 |
| 0,19 | 4,1859 | 0,39 | 4,5797 | 0,59 | 5,0785 | 0,79 | 5,6428 | 0,99 | 6,2518 |
Развертка цилиндра эллиптического, усеченного наклонной плоскостью.
Графически развертка цилиндра (рис. 3) строится следующим образом. На одной четверти горизонтальной проекции эллиптического цилиндра (эллипса) наносится определенное число точек и строятся симметричные им точки и в остальных четвертях (в данном случае эллипс разделен на 12 частей). Из точек деления проводятся вертикальные прямые до пересечения верхнего основания в точках 0Ꞌ1, 1Ꞌ1, …, 12Ꞌ1. На продолжении прямой 9Ꞌ3Ꞌ начиная от точки 0° последовательно откладываются длины дуг эллипса 01, 12, …, 1112. Расстояние 0°12° равно полной длине эллипса (графическое определение длины дуги эллипса показано на рис. 2). Из точек 0°, …, 12° проводятся перпендикуляры до пересечения с горизонтальными линиями, проходящими через точки 0Ꞌ1, …, 12Ꞌ1 в точках 001, …, 1201. Полученные точки соединяются плавной кривой.

Рис. 2.
Графически развертку можно построить еще таким способом. Вокруг эллипса описывается окружность радиусом, равным большой полуоси α (рис. 3). Она делится на определенное число частей, в данном случае на 12. Через точки деления проводятся вертикальные прямые до пересечения с эллипсом в точках 0, 1, …, 12, которые принимаются за точки деления эллипса. Длина дуг эллипса откладывается последовательно на выбранной прямой (в данном случае 0°12°). На расстоянии h1 = (Н — h)/2 от прямой 0°12° проводится горизонтальная прямая. Из центра S, лежащего на прямой, описывается полуокружность радиусом А = (H — h)/2. Полуокружность делится на равные части. Число частей равно половине числу делений окружности, описанной вокруг эллипса. Через точки деления полуокружности 0ꞋꞋ 1ꞋꞋ, … проводятся горизонтальные прямые до пересечения с вертикальными, проходящими через точки 00, …, 120, в точках 001, …, 1201. Полученные точки соединяются плавной кривой.
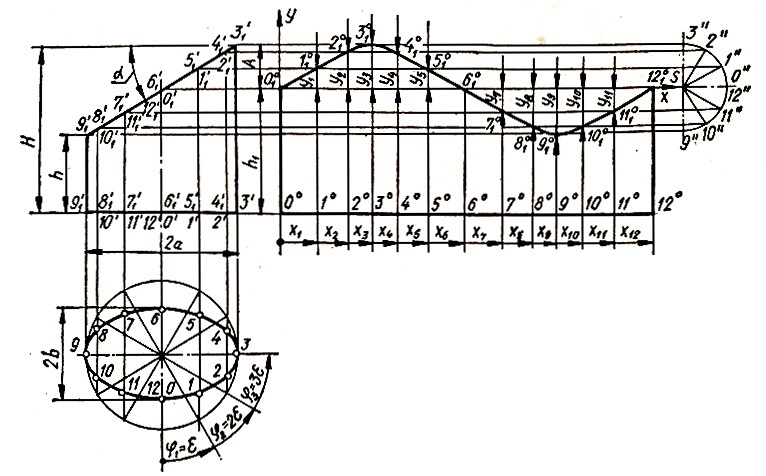
Рис. 3.
Аналитически координаты кривой развертки эллиптического цилиндра, усеченного плоскостью. можно определить, используя данные табл. 2 и 3, а также следующие зависимости:
xk = OK = af (φk, b/а);
yk = A sin kε,
где x и y — координаты точек развертки;
k — порядковый номер точки;
ОК — длина дуги эллипса от точки 0 до произвольной точки К;
а, b — большая и малая полуоси дуги эллипса;
φk = kε — центральный угол между соответствующими точками дуги;
ε = 360°/2n — центральный угол, соответствующий одному делению;
А = (H — h)/2 = a tg α;
2n — число равных делений окружности, описанной около эллипса.
Таблица 2. Значения функции f (φ, b/а) для вычисления длины дуги эллипса.
| Число частей эллипса при 2n | ϕ | b/a | |||||||||
| 12 | 24 | 48 | 0,20 | 0,24 | 0,30 | 0,35 | 0,40 | 0,45 | 0,50 | 0,55 | |
| — | — | 1 | 7,5° | 0,13054 | 0,13054 | 0,13055 | 0,13057 | 0,13058 | 0,13060 | 0,13062 | 0,13063 |
| — | 1 | 2 | 15° | 0,25894 | 0,25900 | 0,25918 | 0,25930 | 0,25943 | 0,25943 | 0,25957 | 0,25973 |
| — | — | 3 | 22,5° | 0,38308 | 0,38331 | 0,38361 | 0,38400 | 0,38430 | 0,38474 | 0,38527 | 0,38575 |
| 1 | 2 | 4 | 30° | 0,50098 | 0,50154 | 0,50221 | 0,50300 | 0,50392 | 0,50494 | 0,50609 | 0,50735 |
| — | — | 5 | 37,5° | 0,61069 | 0,61180 | 0,61313 | 0,61469 | 0,61650 | 0,61853 | 0,62083 | 0,62325 |
| — | 3 | 6 | 45° | 0,71057 | 0,71298 | 0,71486 | 0,71761 | 0,72077 | 0,72431 | 0,72822 | 0,73250 |
| — | — | 7 | 52,5° | 0,79902 | 0,80216 | 0,80601 | 0,81048 | 0,81558 | 0,82122 | 0,82754 | 0,83440 |
| 2 | 4 | 8 | 60° | 0,87492 | 0,87983 | 0,88573 | 0,89259 | 0,90036 | 0,90897 | 0,91839 | 0,92857 |
| — | — | 9 | 67,5° | 0,93736 | 0,94481 | 0,95378 | 0,96360 | 0,97491 | 0,98786 | 1,00085 | 1,01531 |
| — | 5 | 10 | 75° | 0,98626 | 0,99704 | 1,00973 | 1,02411 | 1,04003 | 1,05782 | 1,07586 | 1,09550 |
| — | — | 11 | 82,5° | 1,02261 | 1,03818 | 1,05659 | 1,07643 | 1,09751 | 1,12060 | 1,14504 | 1,17068 |
| 3 | 6 | 12 | 90° | 1,05050 | 1,07227 | 1,09648 | 1,11483 | 1,15066 | 1,18016 | 1,21106 | 1,24310 |
Продолжение таблицы 2. Значения функции f (φ, b/а) для вычисления длины дуги эллипса.
| Число частей эллипса при 2n | ϕ | b/a | |||||||||
| 12 | 24 | 48 | 0,60 | 0,65 | 0,70 | 0,75 | 0,80 | 0,85 | 0,90 | 0,95 | |
| — | — | 1 | 7,5° | 0,13066 | 0,14068 | 0,13071 | 0,13073 | 0,13076 | 0,13079 | 0,13083 | 0,13087 |
| — | 1 | 2 | 15° | 0,25990 | 0,26009 | 0,26029 | 0,26050 | 0,26073 | 0,26097 | 0,26124 | 0,26150 |
| — | — | 3 | 22,5° | 0,38684 | 0,38698 | 0,38764 | 0,38836 | 0,38914 | 0,38996 | 0,39083 | 0,39173 |
| 1 | 2 | 4 | 30° | 0,50873 | 0,51022 | 0,51181 | 0,51352 | 0,51533 | 0,51725 | 0,51926 | 0,52138 |
| — | — | 5 | 37,5° | 0,62594 | 0,62883 | 0,63193 | 0,63532 | 0,63872 | 0,64239 | 0,64625 | 0,65029 |
| — | 3 | 6 | 45° | 0,73714 | 0,74211 | 0,74741 | 0,75302 | 0,75894 | 0,76512 | 0,77163 | 0,77839 |
| — | — | 7 | 52,5° | 0,84168 | 0,84952 | 0,85782 | 0,86658 | 0,87575 | 0,88534 | 0,88530 | 0,90545 |
| 2 | 4 | 8 | 60° | 0,93946 | 0,95100 | 0,96317 | 0,97592 | 0,98922 | 1,00302 | 1,01731 | 1,03204 |
| — | — | 9 | 67,5° | 1,03066 | 1,04608 | 1,06372 | 1,08132 | 1,09956 | 1,11839 | 1,13780 | 1,14771 |
| — | 5 | 10 | 75° | 1,11618 | 1,13777 | 1,16021 | 1,18310 | 1,20732 | 1,23189 | 1,52705 | 1,28276 |
| — | — | 11 | 82,5° | 1,19740 | 1,22510 | 1,25268 | 1,28401 | 1,31319 | 1,34398 | 1,37540 | 1,40738 |
| 3 | 6 | 12 | 90° | 1,27636 | 1,31052 | 1,34559 | 1,38147 | 1,41808 | 1,45537 | 1,49329 |
1,53278 |
Таблица 3. Значения sin kε и sin2 kε.
Данные значений sin kε и sin2 kε Вы можете найти в предыдущей статье: Построение развертки цилиндра. Развертка усеченного цилиндра. Формула развертки цилиндра.

1 комментарий
makar
23.02.2018 в 13:15 (UTC 3) Ссылка на этот комментарий
Очень полезная статья. Те кто знает тот поймет. Если все правильно разобрать то можно все правильно сделать.