Наклонная пирамида развертка. Усеченная четырехгранная пирамида.

Наклонная усеченная пирамида с четырехугольным основанием показана на рис. 1.

Через точки 0′, 0′₁ и 2′, 2′₁ проводятся прямые до пересечения в точке V’, являющейся вершиной пирамиды.

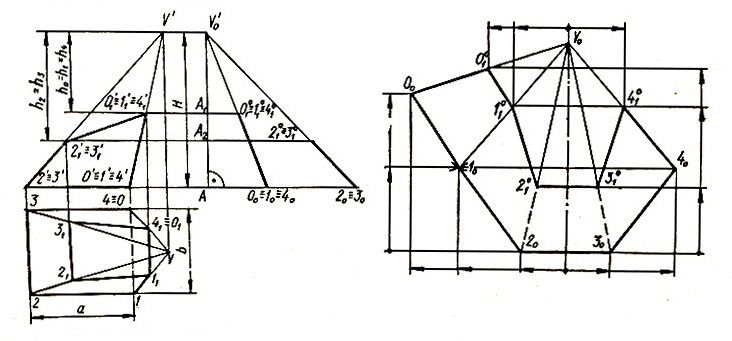
Рис. 1.

Для определения действительном длины ребер пирамиды через произвольную точку А проводят две перпендикулярные прямые. На горизонтальной линии от точки А откладываются расстояния V₀, V₁,…,V₄ до точек 0₀, 1₀, 2₀,…,4₀. На вертикальной линии откладывается высота пирамиды Н до точки V’₀. Расстояния 0₀V’₀, 1₀V’₀,…, 4₀V’₀ представляют собой действительные длины ребер. Для построения развертки необходимо из произвольной точки V₀ отложить отрезок V₀0₀ = V’₀0₀. Из центров V₀ и 0₀ радиусами соответственно V₀1₀ = V’₀1₀ и 0₀1₀ = 01 описываются дуги до пересечения в точке 1₀. Из центров V₀ и 0₀ описываются дуги радиусами V₀2₀ = V’₀2₀ и 1₀2₀ = 12 до пересечения в точке 2₀. Построение продолжается по описанному способу до получения точки 4₀. Точки 1₀, 2₀, 3₀ и 4₀ последовательно соединяются между собой и каждая с V₀.

Развертка усеченной пирамиды четырехугольной.

Действительная длина ребер малого основания определяется следующим образом. От точки V’₀ откладываются расстояния h₀ = h₁ = h₄ до точки А₁ и h₂ = h₃ до точки А₂. Через точки А₁ и А₂ проводятся горизонтальные прямые до пересечения V’₀0₀ и V’₀2₀ в точках 0⁰₁ = 1⁰₁ = 4⁰₁ и 2⁰₁ = 3⁰₁. Из центра V₀ радиусом V’₀0⁰₁ описывается дуга до пересечения V₀0₀, V₀1₀ и V₀4₀ соответственно в точках 0⁰₁, 1⁰₁ и 4⁰₁. Радиусом V’₀2⁰₁ из центра V₀ описывается дуга до пересечения V₀2₀ и V₀3₀ в точках 2⁰₁ и 3⁰₁, Полученные точки 0⁰₁, 1⁰₁, 4⁰₁ последовательно соединяются, расстояния 0⁰₁1⁰₁, 1⁰₁2⁰₁ являются действительными длинами ребер малого основания.